Scientists and Singularities
One of the main driving forces behind the development of science since its creation during the renaissance and reformation periods, has been the attempt to produce complete generality in the formulation of the laws of nature. Until very recent times it was held as an unquestioned belief that ultimately all nature could be reduced to the operation of a few, carefully defined, physical laws of complete generality and universality.
This assumption inevitably led to the mathematical formulation of physical laws as differential equations whose various solutions contained all the possible physical situations. These could be sorted out in particular cases by reference to the particular circumstances, or what are called boundary conditions, for each given situation.
Such a view of the world necessarily entailed the exclusion of all singularities. These included those inexplicable phenomena which did not fit the pristine, general laws and those singular solutions to differential equations which were defined away as “unphysical” or “irrational.”
Since explaining and controlling are closely associated, scientists’ obsession with explaining the world may well indicate an irrational and dangerous compulsion to control everything.
Classical Physics
Classical physics began with Galileo and Newton who regarded the matter of the Heavens as essentially the same as the matter on the Earth’s surface and inside the Earth and therefore subject to the same laws of motion. The guiding maximum of these reductionist scientists was “as below, so above.” This was in direct opposition to the medieval cosmology which had taken from the Greeks the assumption that different laws of motion applied to heavenly bodies as compared with earthly matter.
Like Galileo, Newton abandoned both the geocentric Christian cosmology as a whole metaphysical system and Kepler’s revised “intermediate” metaphysical cosmology. (Kepler had identified the prime mover of the new heliocentric system as both the sun and God the Father, The planets he believed to be the sons of God and the force which the sun exercised over them was the Holy Spirit). Newton therefore desperately needed a fixed frame of reference in which his new laws of motion could operate.
Newton’s Singularity
Newton devised a frame which he called “the absolute frame” which was defined tautologically as that frame in which his laws of motion held perfectly. To give it metaphysical authority he claimed that it corresponded in some undefined way with “the Mind of God.” This was a Unitarian, theistic conceptualisation that differed significantly from Kepler’s mystical Trinitarian approach to metaphysics. Here at the core of Newton’s theory, which emphatically rejected non-universalistic principles in physics, was a great singularity.
The Great Work Continues
In spite of this great metaphysical flaw in classical physical cosmology the eighteenth and nineteenth century scientists pressed blindly on with the great work of reducing the whole complex system of the universe down to a few differential equations. In the course of this programme Maxwell’s equations for electromagnetism reduced light and all other electromagnetic phenomena to four equations and Boltzmann, Maxwell and Gibbs reduced all thermodynamic phenomena to statistical principles applied to atoms and molecules.
Einstein’s Singularity
There still remained, however, the problem of reconciling Maxwell’s equations with the absolute space and time of Newton’s cosmology and it was the pursuit of a solution to this problem which led Einstein to propose the theory of special relativity. Einstein founded his theory upon a new absolute, the “Speed of Light”. The speed of light is postulated to be invariant for all observers. However this axiom is an assumption which simply cannot be explained in terms of the theory. It is both an act of faith and a singularity.
The actual value of the speed of light is not assumed by the theory but, more importantly, what is assumed is its invariance under Lorentz transformations. In just the same way Newton had assumed the existence of absolute space and time which were invariant under Galilean transformations. Modern definitions of distance and time based upon the light radiated by certain atomic transitions are closer to actually defining the speed of light than to measuring light or anything else measured by it.
Trying to Eradicate the Centre of the Universe
In general relativity, which is Einstein’s theory of gravitation and cosmology, mathematical singularities emerge very clearly. In particular it is impossible, within general relativity, to remove a singularity of cosmological importance, this is the point at which the big bang of the universe began. Indeed we can once again envisage experiments in which it is possible to measure our absolute velocity relative to this singular point. This great cosmological singularity provides an absolute reference point or centre of the universe which Einstein had tried so hard to eradicate through relativity theory.
In general relativity frames of reference are still invariant under Lorentz transformations only, but a great deal of more theoretical work suggests that any future theory will have frames of reference which are conformally invariant. This is a more general and less restricted way of transforming coordinates than through the Lorentz transformations. The Maxwell equations are already conformally invariant.
The Almighty Equation Replaces Almighty God
The development of physics in this century seems to have been concentrated upon a search for more and more general transformations being applied to less and less particular coordinate systems. This fits in with the original great work of producing equations of increasing generality. However the more general and all-embracing the equations become, in other words the more general the invariance, the more the equations themselves become unique or singular. Almighty God, the monotheistic medieval singularity and prime-mover, is replaced by the almighty equation.
The Inside-Out Model of the Universe
Attempts to widen the descriptive power of the laws of physics have resulted in a narrowing of the range of possibilities for the form of the laws themselves and hence a greater singularity in the laws. It now seems likely that all of the laws of physics can be made into a conformally invariant form. In other words the laws would remain the same when the coordinate system used to describe the whole universe or world system are subjected to a simple conformal transformation. In this conformal transformation, known as inversion geometry, the defined measuring unit for distance is able to change in a regular way from one point to another but angle measurements remain unchanged.
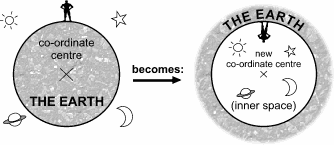
Figure 1: Pictorial representation of the transformation.
A frame of reference is first selected. The one chosen here being the geocentric model with the frame of reference placed with its centre at the centre of the earth. This is an acceptable model within the terms of reference of general relativity. Inversion geometry is then applied to this frame of reference. As a result we obtain a universe which is totally inverted or turned “inside out.”
In the geoperipheral model we perceive ourselves as living on the inside of a sphere, which is the biosphere or surface of the earth, with the ground beneath our feet extending to “infinity” and in the ‘inner space’ above us, inside the earth’s surface, are the sun, moon, planets, galaxies etc…
Immediately the inside-out universe is described, dozens of objections to it are apparent. The well-known phenomenon of the ship disappearing “hull-down” on the horizon; why can’t we in New Zealand see right across to Spain? Where are the sun and the stars, and why are we not burnt up by their heat if they are contained within the hollow earth? The shape of the earth’s shadow on the moon; and so on. These, and a hundred other objections are easily explained in the new model.
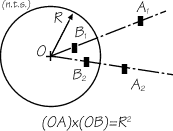
Figure 2: This diagram shows the basis of the theory.
The basis of the conformal transformation is illustrated in Fig. 2. If a point A outside a circle is taken at a distance OA from the centre, it is obvious that another point B can be found inside the circle, at a distance OB from the centre, such that (OA) x (OB) is equal to the square of the radius of the circle. The point B is then said to be the geometrical inverse of the point A.
In a similar manner any number of points outside the circle can be transferred to the inside as geometrical inverses, and so lines and figures outside can be transferred inside. Fig. 3 shows how this transformation appears for some simple figures.
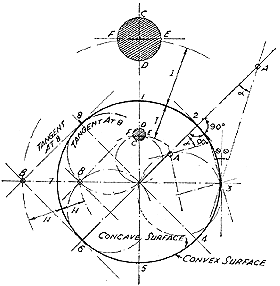
Figure 3.
One or two points about the type of field this inversion geometry produces inside the circle are immediately apparent. In the first place it will be seen that for every point outside the circle there is a corresponding point inside, so that the whole of the space outside can be got into the space within the circle. Again, it can be seen that as the point A recedes from the centre, the point B approaches it, but B only reaches the centre when the point A recedes to “infinity”; therefore, the centre is the geometrical inverse of “infinity”.
A further and most important point, which is not at first apparent but follows logically, is that if lines of sight outside the circle are transferred inside, their directions as seen by an observer on the surface are not altered. Thus if we imagine an observer on the outside, i.e. in orthodox space, at the point 3 (Fig. 3), he sees an object A at an angle (theta) above his horizon. His geometrical inverse on the inside sees the geometrical inverse of A at the same angle (theta) from his horizon.
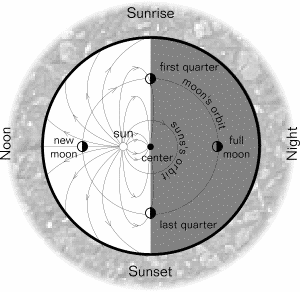
Figure 4 – Explanation of day and night.
In the geoperipheral model the sun and moon both revolve round the co-ordinate centre at an apparently very short distance from it and are considerably diminished in apparent size. The sun revolves around the centre every twenty-four hours with the moon. The moon gains in position relative to the sun and completes an additional orbit each lunar month. The planets have more complicated movements with the outer planets: Mars, Jupiter, Saturn, Neptune, Uranus and Pluto, revolving around the co-ordinate centre, and the inner planets, Mercury and Venus, revolving round the Sun. These are shown, considerably enlarged for illustrative purposes, in the diagram. Note that the earth’s surface surrounds this system and is located at a considerably greater distance away from the limit edge of the diagram that can be shown on this scale.
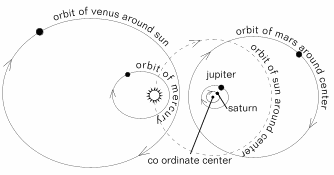
Figure 5 – The orbits of the Sun and planets.
It is possible for the apparently small hollow earth to contain these apparently large objects because the distance scale we are using as a measure changes rapidly as we move it towards the centre of the new co-ordinate system. A measuring rod which is moved into the centre would rapidly decrease in size. Hence objects which are measured by this rod still appear to be immensely large.

Figure 6: The “hull-down” phenomenon. View the image upside down for the orthodox theory.
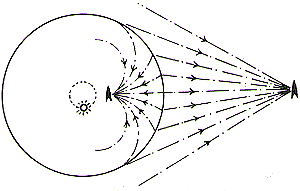
Figure 7 The earth as seen from a space ship in both models
Heaven Reappears in Cosmology
The most interesting aspect of this model is its creation of a single great singularity at the co-ordinate centre near which most of the matter of the universe is concentrated. The apparently most distant parts of the universe are closest to the centre and the distant galaxies, which are moving rapidly away from the surface of the Earth, are all converging upon this central point in inner space.
The adoption of the inverted universe as a model creates a definite centre which can be referred to from all points on or above the Earth’s surface and which is located at the physically “highest” point for all possible observers. Moreover this centre is located in a consistent geometrical position. These qualities are precisely those sought for by pre-scientific metaphysicians when attempting to describe the great supra-mundane singularity referred to by such names as paradise or heaven.
Metaphysical speculation was cut off from physical speculation in the universities by the adoption of the reductionist Newtonian and Einsteinian physical cosmologies. It could be said that the great singularity was “repressed” from consciousness and therefore assumed eccentric and malevolent forms. The obvious failings of the Aristotelian model, modified by Aquinas and other scholastics, have now been corrected without doing violence to the laws of modern physics.
To reconstruct a satisfactory non-fragmented, non-reductionist, and non-eccentric cosmology which includes findings in all fields of intellectual endeavour is without doubt the most important task for the present generation of thinkers.
A start was made in this direction by the Wizard who produced an outline in 1972 which was taught as an experimental, non-accredited, course at the University of Melbourne in 1973, and at the Christchurch Polytechnic in 1975.
In 1997 the Wizard began putting the post-modern cosmology on his web-site.
THE NEXT STEP
Having outlined the nature of this new model of the physical universe and opened it up for discussion, the next step is to outline some of the reasons why this model should be adopted by the human race at this particular time in history.

